Número del envío: 1807
ID del envío: 1816
Submission UUID: e3c34252-ffaf-40a2-84a7-074ec19ffb2d

Created: Dom, 27/11/2022 - 21:15
Completed:
Changed: Dom, 27/11/2022 - 22:03

Remote IP address: (desconocido)
Enviado por: Mariana Garcia
Idioma: Español

Is draft: Sí
Página actual: Vista previa
Form Ficha Terminológica: Ficha Traductológica
Término
lattice
Inglés (Estados Unidos) (214)
Ciencias Físico - Matemáticas y de las Ingenierías (404)
Física (441)
Cristalografía
An array of points in space such that each point is in an identical point environment. Thus, any straight line drawn between any two points in a lattice and continued will pass at equal intervals through a succession of similar points.
(S/f-b). Mindat.org. Recuperado el 28 de noviembre de 2022, de https://www.mindat.org//glossary/lattice
In the general case, the formal definition of a perfect three-dimensional bulk crystal starts from a three-dimensional periodic arrangement of atoms. Here, the crystal periodicity is described by a lattice with lattice vectors R1, R2, R3. Thus, the lattice forms an infinite and periodic array of lattice points reached from a common origin by vectors R with R = n1 R1 + n2 R2 + n3 R3 (2:19) where the coefficients n1, n2, n3 can assume any integer value.
Hermann, K. (2011). Crystallography and surface structure : an introduction for surface scientists and nanoscientists. Wiley-VCH.
Español
red cristalina
Nominal (221)
México (Mex.) (192)
Es una distribución periódica regular de puntos en el espacio. La estructura cristalina se forma cuando se une una base de átomos de forma idéntica a todos los puntos de la red.
Kittel, C. (1995). Introducción a la física del estado sólido. Reverté. Recuperado el 25 de noviembre de 2022 de shorturl.at/dgu57
La periodicidad es una propiedad fundamental de la red cristalina. La periodicidad se define como la repetición de motivos en intervalos determinados de la red cristalina, para explicar la periodicidad debemos localizar vectores no colineales (en un mismo plano) en una red bidimensional; la combinación de los vectores nos daría el vector resultante que lo llamaremos vector fundamental.
Hernandez, H. F. C., Yepes, P. N. M., & Sanchez, H. A. V. (2006). Fundamentos de cristalografía. ELIZCOM SAS. Recuperado el 25 de noviembre de 2022 de shorturl.at/eors9
Multimedia
imagen_2022-11-27_220039855.png
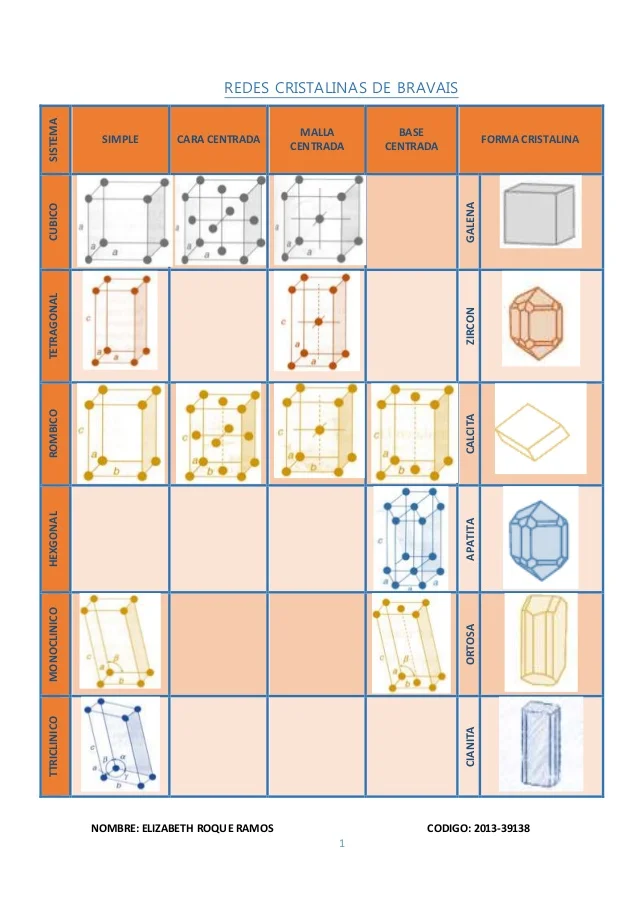
Externa
https://pt.slideshare.net/minzyhyun/redes-de-bravais-49153502
Notas para la traducción
enrejado
Para evitar la repetición del adjetivo, hay autores que tan solo escriben red cristalina al inicio para plantear el referente y después lo recuperan solamente con red.
Descargar PDF